Currently, I mainly think of developing biologically plausible models of neuronal systems and evolutionary processes,
mathematically and computationally studying their dynamic behavior, verifying their predictions using experimental data,
and finally providing explanations that are biologically meaningful and useful.
Theoretically, I am interested in analyzing the solutions and long-term behavior of evolutionary PDEs and systems of ODEs that model biological networks.
Below are some of the research projects I have been working on in recent years.
|
|
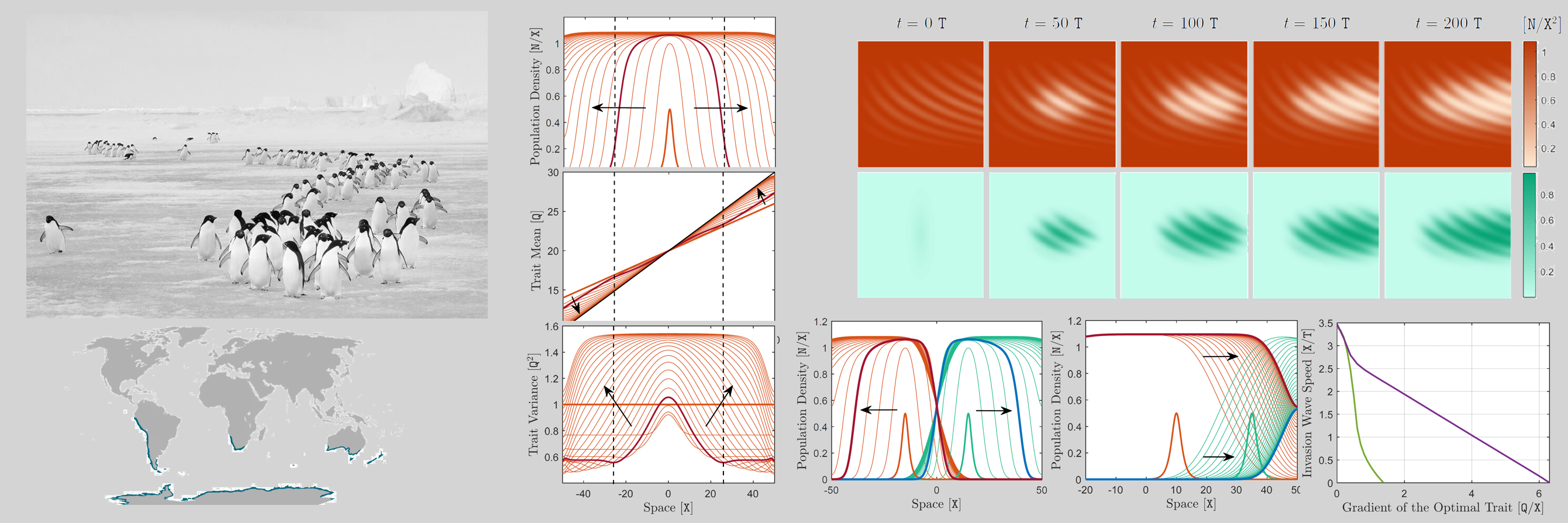
Evolution of a Species' Range |
|
This has been an interesting research area I started working in after I received my PhD, which is in fact entirley different from what I did in my PhD thesis.
In this area, my collaborators and I have been developing and analyzing PDE models of species range evolution.
The models we have developed jointly capture the dynamic changes in species' spatial population densities and the selective evolution of fitness-related phenotypic traits within
the populations, in the presence of an environmental gradient.
We have made a lot of effort to carefully suggest biologically reasonable ranges of values for the parameters of the models,
which is essential for interpreting and comparing predictions of these types of models.
There has been a long-standing hypothesis in the literature, known as "genetic swamping",
that the intraspecific feedback between core-to-edge maladaptive gene
flow and population density of a species can limit its range.
Although not completely conclusive yet, our findings so far suggest that range pinning is unlikely to occur due to genetic swamping though.
Instead, our results have reaffirmed interspecific competition as an effective factor in limiting species' ranges.
The models and results we have developed so far can be found
here.
We have extended our models to study the effects of different dispersal strategies on adaption and range expansion of a species.
Our analysis of the extended models have resulted in very interesting predictions.
I will post the results here as soon as we finish a draft.
|
|
Coordination, Balance, and Robustness of Cortical Activity in the Brain |

|
Stability and excitability are essential properties of cortical networks that are established through complicated dynamic interactions between neurons.
If the recurrent excitation provided by the population of excitatory neurons on itself is not sufficiently balanced by the inhibition it receives from inhibitory neurons,
then the overall level of excitation in the network can rapidly rise to an extreme level at which the spiking rates of the neurons saturate.
Oppositely, if the inhibitory neurons impose excessive inhibition on the excitatory population,
the network loses the level of excitability that it needs to effectively respond to inputs coming from other cortical areas.
Hence, maintaining an overall balance of excitation and inhibition in cortical networks is crucial for their functionality and normal operation.
It has been hypothesized that the balance of excitation and inhibition is essential for controlling network-level information transmission, efficient,
high-precision, and high-dimensional representations and processing of sensory information,
enabling cortical computations by enhancing the range of network sensitivity to sensory inputs,
selective amplification of specific activity patterns in unstructured inputs,
maintaining information in working memory, and, importantly, preserving network stability.
Pathological conditions resulting in deviations from normal levels of excitation-inhibition balance,
hence hypo- or hyper-excitation in cortical networks,
have been associated with several neurological disorders, such as Autism Spectrum Disorders,
schizophrenia, mood disorders, Alzheimer’s disease, Rett Syndrome, and epilepsy.
I have been using and developing biologically plausible mathematical models to theoretically identify the anatomical and physiological factors
that contribute to the balance and coordination of activity in the neocortex at multiple scales,
investigating the robustness of neocortical functionality with respect to changes in these factors, and identifying the pathological brain states that can result from
substantial deviation of such factors from their normal conditions.
My preliminary findings so far, based on an extensive computational study of the effects of physiological and structural factors on the
balance of excitation and inhibition in local cortical networks, can be found
here,
and also, to some extent,
here.
|
|
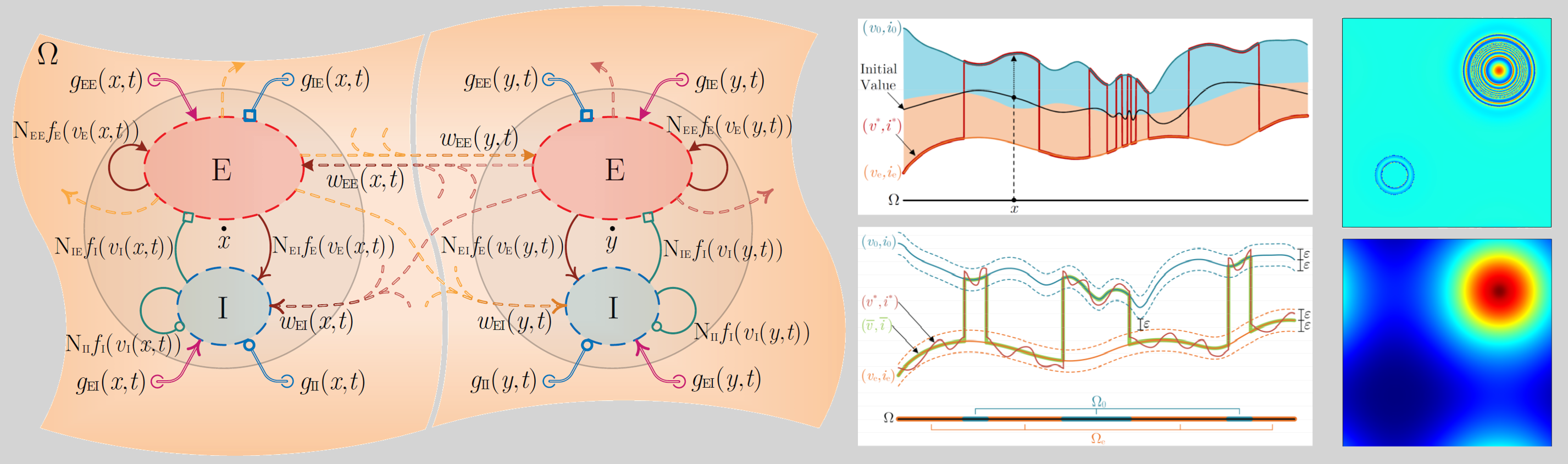
Global Dynamics of an Electroencephalographic Mean Field
Model of the Neocortex |
|
My doctoral research was on mathematical and computational analysis of a mean field model of EEG activity in the neocortex.
The model is composed of a system of coupled ODE and PDE equations.
Presence of nonlinear ODE equations, being coupled with damped wave equations,
made the analysis of the regularity of the solutions and global dynamics of the model subtle.
My work was the first effort to establish rigorous analytical results on well-posedness, regularity, and global dynamics of this model
in an infinite-dimensional dynamical system framework.
Unlike usual mathematical works on problems of this nature, I ensured the applicability of the results to neuroscience problems
by carefully including the entire set of 29 biophysical parameters of the model in the analysis,
as well as constraining the analysis by biologically reasonable ranges of values of these parameters.
An important result of my analysis is that, for some sets of biophysical parameter values,
the equilibrium set of the model is not compact, in both the weak and strong topologies I considered for the phase
space of the model. This further implies that the global attracting set of the model is noncompact
for such parameter values.
Therefore, my rigorous mathematical analysis of the model, which involved studying
the dynamics of neocortical activity both in space and time, predicts a very high-dimensional (almost infinite-dimensional)
spatio-temporal dynamics and a rich variety of behavior in the neocortex under certain brain states.
The results of this work can be found
here.
I also used the model to computationally study the emergence of transient spatio-temporal gamma oscillations
induced by neuronal response modulations.
I could identify a plausible mechanism through which gamma oscillations emerge robustly
and transition back to the resting-state low beta oscillations.
The results show that, regardless of the type of modulations used to induce the gamma oscillations,
either excitatory or inhibitory, a subsequent modulation of excitatory populations that reduces the level of excitation
in the cortical network is necessary and sufficient for termination of the emerged oscillations and transition to low beta oscillations.
Moreover, when gamma oscillations are initially induced by modulation of inhibitory populations,
the subsequent necessary modulation of excitatory populations is indeed in the direction of
restoring the balance of excitation and inhibition in the network.
My simulation results further demonstrate that the propagating waves of gamma oscillations can be of very short length compared with
the diameter of a typical EEG electrode.
Consequently, the collective measurements of these waves of activity by an EEG electrode shows significantly
lower amplitude oscillations compared with point-measurements,
which can potentially provide an explanation for the relatively low spectral power of gamma oscillations observed in experimental recordings.
Also, the results show that the temporal pattern of EEG recordings can be substantially affected by
the averaging effect of the electrodes. The details of this wrok can be found
here.
|
|